Design Matrix For Quadratic
This comes from an attempt at using a 3rd-order Newton optimization step. OrF example the identity matrix is always square.
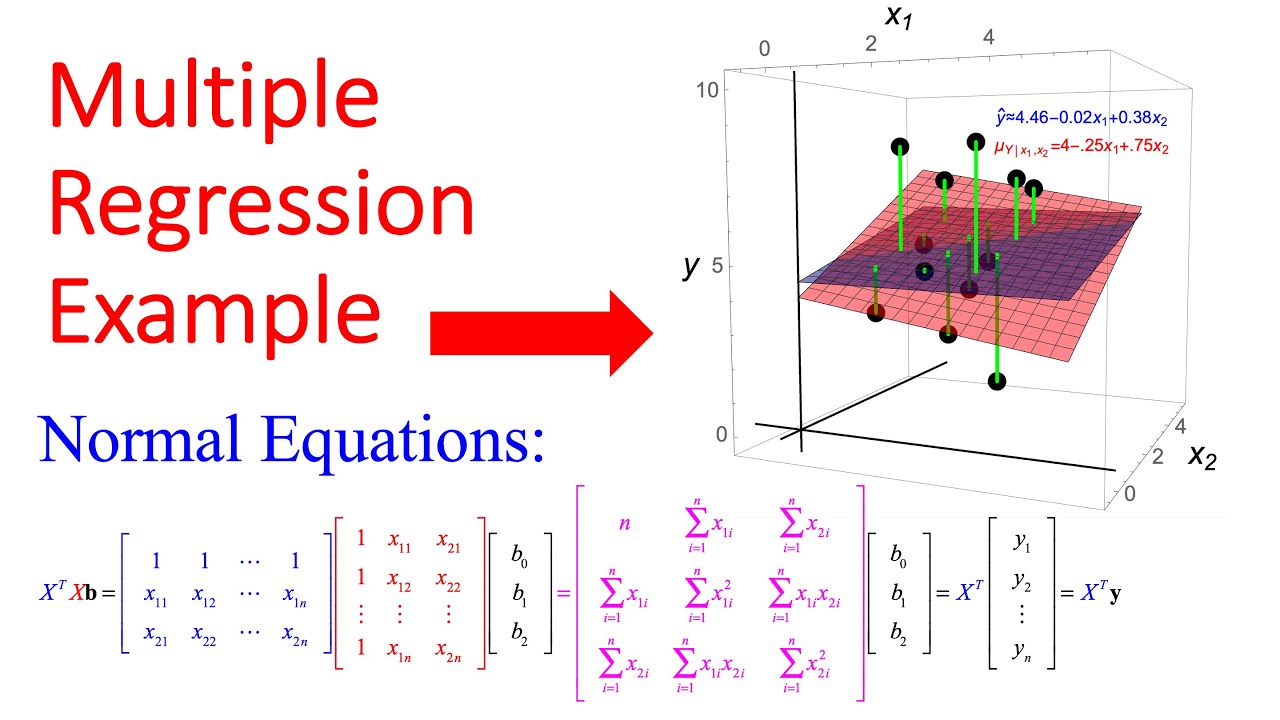
Design Matrix Normal Equations For Simple Multiple Linear Regression Mathematica Spreadsheet Youtube
By default x2fx returns the design matrix for a linear additive model with a constant termmodel is one of the following.

Design matrix for quadratic. The minimal value of the PI using this gain is given by 5 which only. If a square matrix has the property that a ij a ji for all its elements then we call it a. Frank Wood fwoodstatcolumbiaedu Linear Regression Models Lecture 11 Slide 30 ANOVA quadratic forms Consider the following rexpression of bX.
Its general form is minimize fx 1 2 xTBx xTb 31a over x 2 lRn subject. The polynomial regression exam. D x2fxXmodel converts a matrix of predictors X to a design matrix D for regression analysis.
Description KSe lqrSYSQRN calculates the optimal gain matrix K. It is known from linear algebra that if S is symmetric all its eigenvalues are. Recently I was asked about the design matrix or model matrix for a regression model and why it is important.
223 Square Symmetric and ranspTose Matrices A square matrix is a matrix whose number of rows is the same as its number of columns. It is a matrix quadratic equation that can be solved for the auxiliary matrix P given ABQR. The reason it is called the identity matrix is because AI IA A.
In a nutshell it is a matrix usually denoted of size where is the number of observations and is the number of parameters to be estimated. It is a matrix quadratic equation that can be solved for the auxiliary matrix P given ABQR. The ANOVA sums SSTO SSE and SSR are all quadratic forms.
Solving a matrix design equation Obtaining a guaranteed solution that stabilizes the system. Applied Statistics course Advanced Undergraduate Statistics course Lecture 18 Spring 2020 Bethel University St. 61 Quadratic Forms Before we state the optimal control problem we review briefly the concept of quadratic forms.
For x Rn the scalar-valued function xTSx is called a quadratic form associated with S. Its not obvious to me that this value is symmetric. Then the optimal SVFB gain is given by 6.
The minimal value of the PI using this gain is given by. The design matrix is defined to be a matrix such that the j th column of the i th row of represents the value of the j th variable associated with the i th object. The optional input model controls the regression model.
Then the optimal SVFB gain is given by 6. CHAPTER 9 QUADRATIC FORMS SECTION 91 THE MATRIX OF A QUADRATIC FORM quadratic forms and their matrix notation Ifqa 1 x 2 a 2 y 2 a 3 z 2 a 4 xya 5 xza 6 yz then q is called a quadratic form in variables xyz. In simple linear regression ie.
Let S be an n n symmetric matrix ie S ST. We can evaluate quadratic integral exactly by solving a set of linear equations without even computing a matrix exponential Linear quadratic Lyapunov. For a continuous time system the state-feedback law u Kx minimizes the quadratic cost function.
The design matrix originally used included the limits of the factor settings available to run the process. A is the matrix of the quadratic form. Symmetric matrices quadratic forms matrix norm and SVD 1516.
Evaluating quadratic integrals suppose x Ax is stable and define J Z 0 xtTQxt dt to find J we solve Lyapunov equation ATP PAQ 0 for P then J x0TPx0 in other words. Such an NLP is called a Quadratic Programming QP problem. The typical model formulation is.
There i s a q value a scalar at every point. A parameter for the intercept and a parameter for the slope. Chapter 3 Quadratic Programming 31 Constrained quadratic programming problems A special case of the NLP arises when the objective functional f is quadratic and the constraints hg are linear in x 2 lRn.
But this is not always the case where one can simply see how the matrix is going to be so is there a certain method of finding this matrix. Century and used a similar equation in the study of heat flow. To a physicist q is probably the energy of a system with ingredients xyz.
In mathematics a quadratic form is a polynomial with terms all of degree two form is another name for a homogeneous polynomialFor example is a quadratic form in the variables x and yThe coefficients usually belong to a fixed field K such as the real or complex numbers and one speaks of a quadratic form over KIf and the quadratic form takes zero only when all variables are. Ive read some good ideas for computing the square root of symmetric matrices. Ellipsoids if A AT 0 the set E x xTAx 1 is an ellipsoid in Rn centered at 0 s1 s 2 E Symmetric matrices quadratic forms matrix norm and SVD 1517.
A regression model which is a linear combination of the explanatory variables may therefore be represented via matrix multiplication as where X is the design matrix is a vector of the models coefficients one. Distinct predictor variables should appear in different columns of X. Semi-axes are given by si.
Following the traditional quadratic formula approach you end up needing the square root of 1 4 A 1 B A 1 B A 1 C. Equations for quadratic and cubic models In other circumstances a complete description of the process behavior might require a quadratic or cubic model.

The Quadratic Formula Algebra 1 Quadratic Equations Mathplanet Quadratics Quadratic Formula Quadratic Equation
Expressing A Quadratic Form With A Matrix Video Khan Academy

Expressing A Quadratic Form With A Matrix Youtube
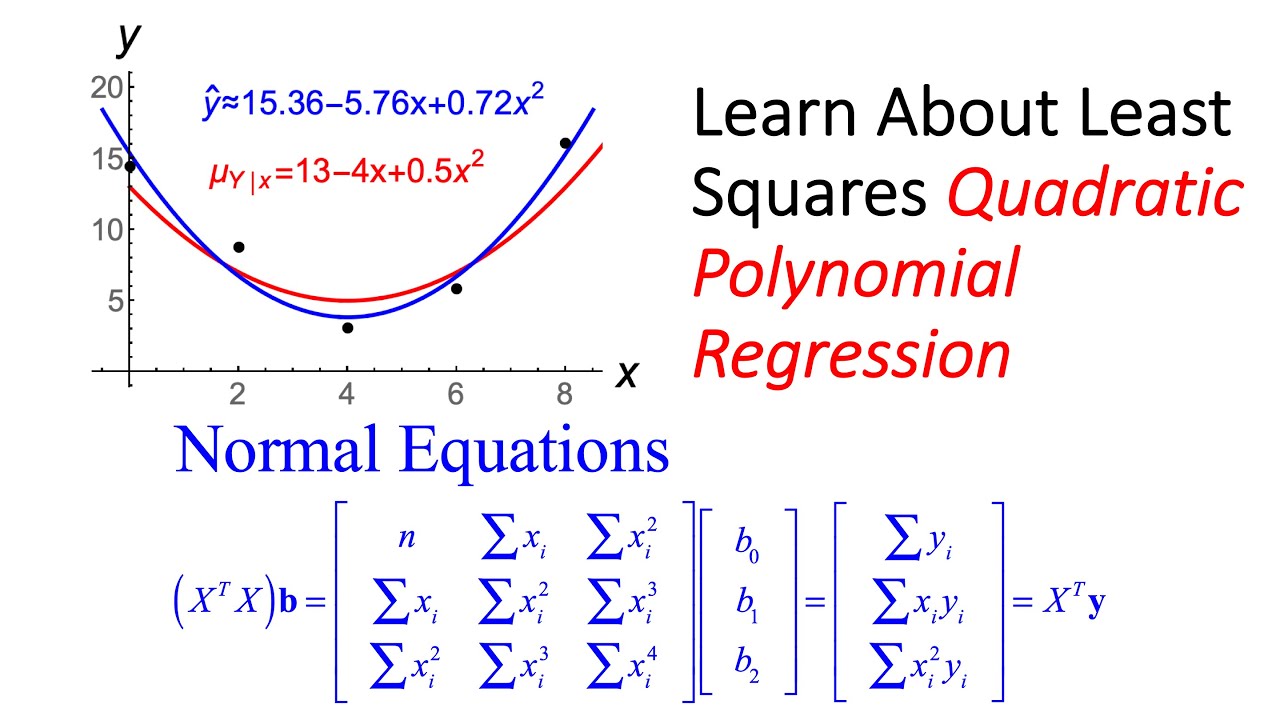
Regression Practical Meaning Quadratic Polynomial Regression Normal Equations Design Matrix Youtube
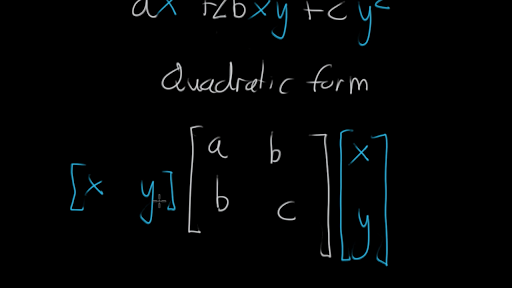
Post a Comment for "Design Matrix For Quadratic"